数理モデルによるCOVID-19の国内の集団免疫割合の推計 | 研究プログラム | 東京財団政策研究所

東京財団政策研究所

SEARCH
詳細検索

東京財団政策研究所

数理モデルによるCOVID-19の国内の集団免疫割合の推計
写真提供：Getty Images

数理モデルによるCOVID-19の国内の集団免疫割合の推計

March 31, 2022

R-2021-074

1. はじめに
2. モデル
3. 結果
4. まとめ

1. はじめに

新型コロナウイルス感染症（COVID-19）が国内で初めて確認されてからすでに2年以上が経過しており、2022年3月現在、国内での感染報告者数は500万を超え[1]、ワクチン接種回数は2億を超えている[2]。このような状況において、同感染症に対する国内の集団免疫割合を推計することは、今後の流行動態を予測する上で重要であると考えられる。本稿では、数理モデルを用いた推計結果を紹介し、それに関する考察を行う。

2. モデル

集団を感受性（Susceptible）、潜伏期（Exposed）、感染（Infectious）、回復（Recovered）の4種類に区分するSEIRモデル[3]を用いる。今回はさらに、ワクチンの接種歴に応じてモデルを細分する。すなわち、SEIRモデルの各集団をワクチン未接種（S, E, I, R）、ワクチン接種1回（S1, E1, I1, R1）、ワクチン接種2回以上（S2, E2, I2, R2）のように分ける。また、ワクチンによる免疫の減衰を考慮するために、ワクチン接種2回以上の集団には齢構造[3]を導入し、2回接種後からの経過時間に応じて免疫が減衰されるが、ブースター接種（3回目以降）が行われると2回接種直後の水準に免疫が回復すると仮定する。

推計に当たって、モデルの感染率とワクチン接種率は時変パラメータとした。具体的に、行動変容やウイルス変異などの様々な要因による感染のしやすさの変化をとらえるために、日ごとの感染率は過去1週間のデータ[1]への曲線当てはめによって決定した。また、接種回数のデータ[2]を利用して日ごとのワクチン接種率を決定した。詳細については[4]を参照されたい。図1に実際の感染報告数（赤点）とモデルにより推定される流行曲線（青線）を示す。

図1 国内のCOVID-19の日ごとの感染報告数（2020/1/14～2022/3/6）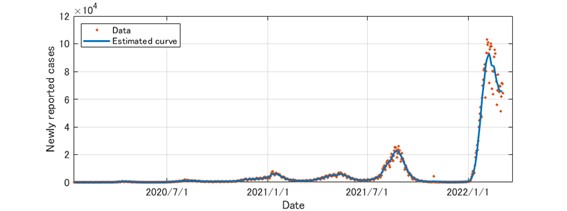

3. 結果

モデルにより推計される国内の日ごとの集団免疫割合を図2に示す。

図2 国内の日ごとの集団免疫割合の推計（2020/1/14～2022/3/6）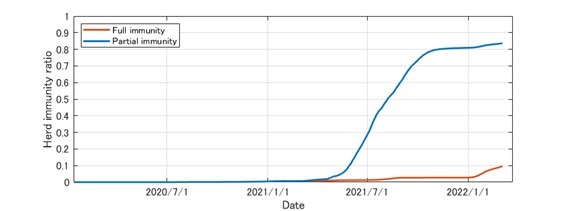

ここで Full immunity（赤線）はワクチン接種経験の有無にかかわらず感染を経験した者の割合を表し、Partial immunity（青線）はそれに加えて感染経験は無いが2回以上ワクチン接種経験のある者の割合を含めたものを表す。図2では、2022年3月上旬の段階で、国内の集団免疫割合（Full immunity）はおよそ1割に到達し、ワクチンによる部分的な免疫を含める（Partial immunity）と、その割合は8割を超えていることが示されている。特に、2022年1月以降のオミクロン株が主流である第6波を経て、集団免疫割合が顕著に増加していることがグラフから読み取れる。一方、部分的な免疫は、ワクチンの一般接種が本格化した2021年6月以降から顕著に増加していることが読み取れる。

4. まとめ

本稿では、流行開始から2年以上を経て、国内のCOVID-19に対する集団免疫割合は確実に増加していることを示す推計結果が得られた。COVID-19の基本再生産数を2.5とする[5]と、基本的な感染症モデルで算出される臨界免疫化割合[3]は 1-1/2.5 = 0.6 であるから、流行が終息する上で十分な集団免疫の達成には至っていないと考えられる。一方で、本稿の推計はあくまで現実を簡略化したモデルに基づいているという点に注意が必要である．特に、本稿のモデルでは感受性が一様な集団を考えているが、異質性を考慮すると、リスクの高い集団の中で集中的に感染が起こるため、流行終息に必要な集団免疫割合がより低くなる可能性が指摘されている[6]。その場合、必ずしも集団免疫割合が0.6に達しなくても流行が終息する可能性があると考えられる。一方で、本稿のモデルではウイルス変異による免疫効果の減少を考慮していないため、集団免疫割合を過大に推計している可能性がある。その他、本稿のモデルの詳細と限界については[4]を参照されたい。

 

参考文献


[1] WHO, Coronavirus (COVID-19) Dashboard, https://covid19.who.int/　2022年3月8日閲覧.
[2] 首相官邸ホームページ, 新型コロナワクチンについて, https://www.kantei.go.jp/jp/headline/kansensho/vaccine.html　2022年3月8日閲覧.
[3] 稲葉寿編, 感染症の数理モデル 増補版, 培風館, 2020年.
[4] T. Kuniya, Appendix to a review article for The Tokyo Foundation for Policy Research, http://www2.kobe-u.ac.jp/~tkuniya/appendix　2022年3月9日閲覧.
[5] N. Imai, et al., Report 3: Transmissibility of 2019-nCoV (2020). https://www.imperial.ac.uk/media/imperial-college/medicine/mrc-gida/2020-01-25-COVID19-Report-3.pdf　2022年３月7日閲覧.
[6] 稲葉寿, 感染症数理モデルとCOVID-19, https://www.covid19-jma-medical-expert-meeting.jp/topic/3925　2022年3月8日閲覧.

注目コンテンツ

BY THIS AUTHOR

この研究員のコンテンツ

0%

PROGRAM-RELATED CONTENT

この研究員が所属するプログラムのコンテンツ

VIEW MORE

DOMAIN-RELATED CONTENT

同じ研究領域のコンテンツ

VIEW MORE

INQUIRIES

お問合せ

取材のお申込みやお問合せは
こちらのフォームより送信してください。

お問合せフォーム